Trees - Linked
//Definition for a binary tree node.
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
Linked List Construction
//Definition for singly-linked list.
struct ListNode {
int val;
ListNode *next;
ListNode(int x) : val(x), next(NULL) {}
};
Tips:
Linked List Problems Mostly relate to Recursion, especially Trees (BST)
Canonical Problems:
LeetCode 206. Reverse Linked List:
Iteration
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* prev = nullptr;
ListNode* curr = head;
ListNode* next;
while (curr) {
next = curr->next;
curr->next = prev;
prev = curr;
curr = next;
}
return prev;
}
};
Recursion
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if (!head || !(head->next)) return head;
ListNode* tmp = head -> next;
ListNode* newNode = reverseList(tmp);
tmp->next = head;
head->next = NULL;
return newNode;
}
};
二分模板
// Returns the smallest m in [l, r),
// s.t. cond(m) == True
// If not found returns r.
def binary_search(l, r, cond)
while l < r:
m = l + (r - l) // 2
if cond(m):
r = m
else
l = m + 1
return l
Recursion 模板
def function(int a){
if cal[a] is True:## memoriztion
return cal[a]
#do something with function(a-1)
cal[a] = function(a-1)+a
return cal[a]
}
排列模板
def P(n, m, cur, used):
if len(cur) == m:
print(cur)
return
for i in range(n):
if used[i]: continue
used[i] = True
cur.append(i + 1)
P(n, m, cur, used)
cur.pop()
used[i] = False
n = 5
m = 3
P(n, m, [], [False] * n)
组合模板
def C(n, m, s, cur):
if len(cur) == m:
print(cur)
return
for i in range(s, n):
cur.append(i + 1)
C(n, m, i + 1, cur)
cur.pop()
n = 5
m = 3
C(n, m, 0, [])
DFS
Notes:
DFS function:
- when void: do not need to deal with returning some value, just focusing on when to finish.
- when some value (like boolean), needs to consider what to return when some condition happens.
DFS: for all neighbors: if (unvisited) DFS();
// Check whether there is a path from |start| to |target| in graph G.
// neighbor(x) returns the neighbors of x in G.
seen = set([start])
def dfs(n):
if n == target:
return True
for t in neighbor(n):
if t in seen: continue
seen.add(t)
if dfs(t): return True
seen.remove(t) # back-tracking
return False
return dfs(start)
DFS Examples: 737. Sentence Similarity II
class Solution {
public:
bool areSentencesSimilarTwo(vector<string>& words1, vector<string>& words2, vector<pair<string, string>> pairs) {
if (words1.size() != words2.size()) return false;
unordered_map<string, unordered_set<string>> p;
for (auto &vp : pairs) {
p[vp.first].emplace(vp.second);
p[vp.second].emplace(vp.first);
}
for (int i = 0; i < words1.size(); i++) {
unordered_set<string> visited;
if (isSimilar(words1[i], words2[i], p, visited)) continue;
else return false;
}
return true;
}
bool isSimilar(string& s1, string& s2, unordered_map<string, unordered_set<string>>& p, unordered_set<string>& visited) {
if (s1 == s2) return true;
visited.emplace(s1);
for (auto s : p[s1]) {
if (!visited.count(s) && isSimilar(s, s2, p, visited))
return true;
}
return false;
}
};
DFS Examples: 200. Number of Islands
class Solution {
public:
int numIslands(vector<vector<char>>& grid) {
if (grid.empty()) return 0;
int m = grid.size();
int n = grid[0].size();
int num = 0;
for (int i = 0; i < m; ++i)
{
for (int j = 0; j < n; ++j)
{
if (grid[i][j] == '1')
{
DFS(m,n,i,j,grid);
num += 1;
}
}
}
return num;
}
private:
void DFS(int m, int n,int r, int c,vector<vector<char>>& grid)
{
if (r < 0 || c < 0 || r >= m || c >= n || grid[r][c] == '0') return;
grid[r][c] = '0';
DFS(m,n,r+1,c,grid);
DFS(m,n,r-1,c,grid);
DFS(m,n,r,c+1,grid);
DFS(m,n,r,c-1,grid);
}
};
BFS
// Find the shortest path from |start| to |target| in a unweighted graph G.
// neighbor(x) returns the neighbors of x in G.
q = deque([start])
seen = set([start])
steps = 0
while q:
size = len(q)
for _ in range(size):
n = q.popleft()
if n == target: return steps
for t in neighbor(n):
if t in seen: continue
q.append(t)
seen.add(t)
steps += 1
return -1 # not found
滚动数组DP模板
void function(N, matrix,m,n)
{
intilize;
vector<vector<int>> dp(...);
for (int k = 0; k < N; ++k)// how many times
{
vector<vector<int>> tmp(...);
for (int i = 0; i < m; ++i)
{
for (int j = 0; j < n; ++j)
{
/* code */
}
}
dp.swap(tmp);
}
return ...;
}
Word Matching DP – 单词 从后往前
class Solution {
public:
bool isMatch(string s, string p) {
int n1 = s.size();
int n2 = p.size();
vector<vector<int>> dp(n1+1,vector<int>(n2+1,0));
dp[0][0] = 1;
// Initialization
for (int i = 1; i <= n1; ++i)
{
dp[i][0] = 0;
}
for (int j = 1; j <= n2; ++j)
{
if (p[j-1] == '*')
{
dp[0][j] = dp[0][j-2];
}
else
{
dp[0][j] = 0;
}
}
// 分情况讨论
for (int i = 1; i <= n1; ++i)
{
for (int j = 1; j <= n2; ++j)
{
if (p[j-1] != '.' && p[j-1] != '*')
{
if (s[i-1] != p[j-1])
{
dp[i][j] = 0;
}
else
{
dp[i][j] = dp[i-1][j-1];
}
}
else if (p[j-1] == '.')
{
dp[i][j] = dp[i-1][j-1];
}
else if (j >= 2)
{
if (p[j-2] == s[i-1])
{
dp[i][j] = (dp[i-1][j-2] || dp[i][j-2] || dp[i-1][j]);
}
else if (p[j-2] != '.')
{
dp[i][j] = dp[i][j-2];
}
else
{
dp[i][j] = (dp[i-1][j-2] || dp[i][j-2] || dp[i-1][j]);
}
}
}
}
return dp[n1][n2] > 0 ? true:false;
}
};
Binary Tree Traversal 模板
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
order(root);
return ans;
}
private:
void order(TreeNode* root)
{
if (root == NULL)
{
return;
}
order(root -> left);
order(root -> right);
ans.push_back(root-> val);
return;
}
vector<int> ans;
};
Save Memory of run-time stack;
前缀树模板
class Trie(object):
def __init__(self): self.root = {}
def insert(self, word):
p = self.root
for c in word:
if c not in p: p[c] = {}
p = p[c]
p['#'] = True
def search(self, word):
node = self._find(word)
return node and '#' in node
def startsWith(self, prefix):
return self._find(prefix)
def _find(self, prefix):
p = self.root
for c in prefix:
if c not in p: return None
p = p[c]
return p
Union Find
// Author: Huahua
class UnionFindSet {
public:
UnionFindSet(int n) {
ranks_ = vector<int>(n + 1, 0);
parents_ = vector<int>(n + 1, 0);
for (int i = 0; i < parents_.size(); ++i)
parents_[i] = i;
}
// Merge sets that contains u and v.
// Return true if merged, false if u and v are already in one set.
bool Union(int u, int v) {
int pu = Find(u);
int pv = Find(v);
if (pu == pv) return false;
// Meger low rank tree into high rank tree
if (ranks_[pv] < ranks_[pu])
parents_[pv] = pu;
else if (ranks_[pu] < ranks_[pv])
parents_[pu] = pv;
else {
parents_[pv] = pu;
ranks_[pu] += 1;
}
return true;
}
// Get the root of u.
int Find(int u) {
// Compress the path during traversal
if (u != parents_[u])
parents_[u] = Find(parents_[u]);
return parents_[u];
}
private:
vector<int> parents_;
vector<int> ranks_;
};
Explanation

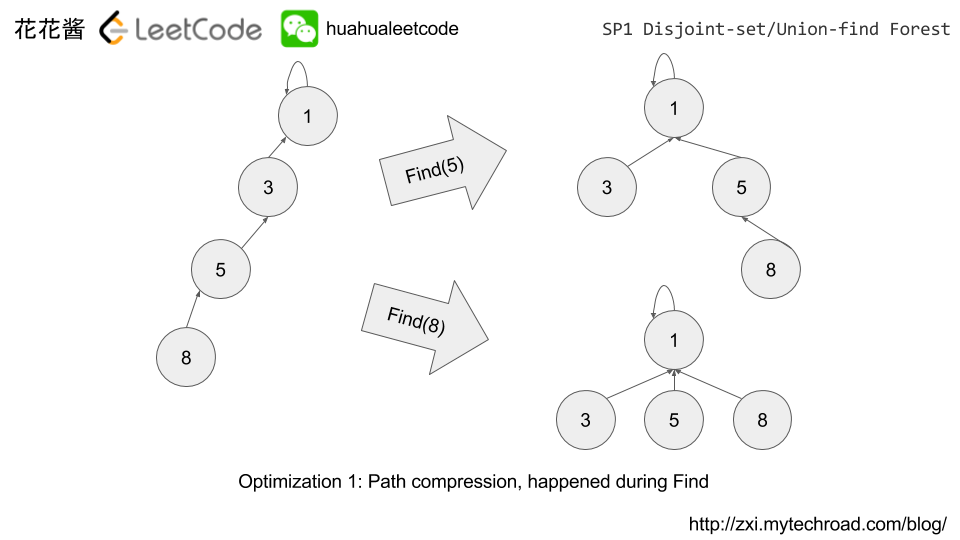
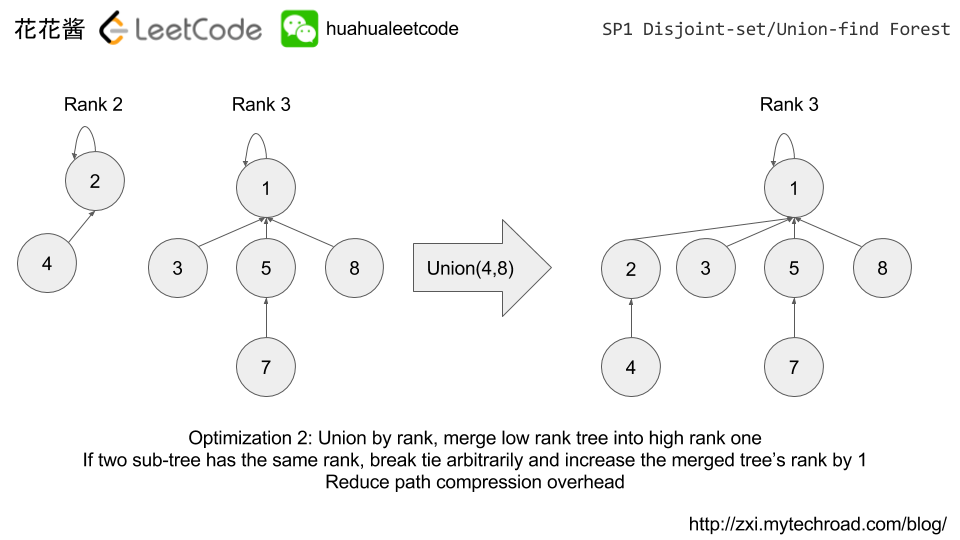
Examples:
-花花酱 LeetCode 547. Friend Circles -花花酱 LeetCode 737. Sentence Similarity II -花花酱 LeetCode 684. Redundant Connection