Summary

• 多状态之间得关系，注意初始条件 DP[i][j] iterate i or j can be reverted 可以反着来，可能更方便

• 滚动数组把循环几轮放在最开始的循环 nested cycles

• DP 分成片段 [a,b] 应对复杂的DP问题 学会额外增加一行一列， 作为初始值，方便计算，0，0

Leetcode Problems

Leetcode Canonical Problems

121. Best Time to Buy and Sell Stock

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        if (n < 2) return 0;
        vector<int> gains(n - 1, 0);
        for (int i = 1; i < n; ++i)
            gains[i - 1] = prices[i] - prices[i - 1];
        return max(0, maxSubArray(gains));
    }
private:
    // From LC 53. Maximum Subarray
    int maxSubArray(vector<int>& nums) {
        vector<int> f(nums.size());
        f[0] = nums[0];
        
        for (int i = 1; i < nums.size(); ++i)
            f[i] = max(f[i - 1] + nums[i], nums[i]);
        
        return *std::max_element(f.begin(), f.end());
    }
};

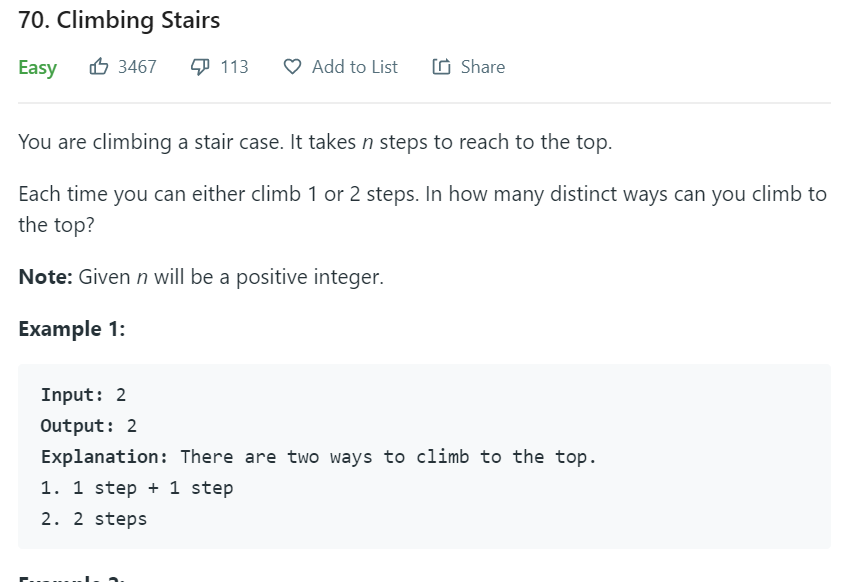
70. Climbing Stairs

class Solution {
public:
  int climbStairs(int n) {
    // f[i] = climbStairs(i)

    int n1, n2, n3;
    n1 = 0;
    n2 = 1;
    // f[i] = f[i-1] + f[i-2]
    for (int i = 1;i <= n; ++i)
    {
        n3 = n1 + n2;
        n1 = n2;
        n2 = n3;
    }
    return n2;
  }
};

53. Maximum Subarray

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        vector<int> f(nums.size());
        f[0] = nums[0];
        
        for (int i = 1; i < nums.size(); ++i)
            f[i] = max(f[i - 1] + nums[i], nums[i]);
        
        return *std::max_element(f.begin(), f.end());
    }
};

198. House Robber

class Solution {
public:
    int rob(vector<int>& nums) {
        if (nums.empty()) return 0;
        int dp1 = 0;   
        int dp2 = 0;
        for (int i = 0; i < nums.size(); ++i)
        {
            int dp = max(dp1, dp2 + nums[i]);
            dp2 = dp1;
            dp1 = dp;
        }
        return dp1;
    }
};

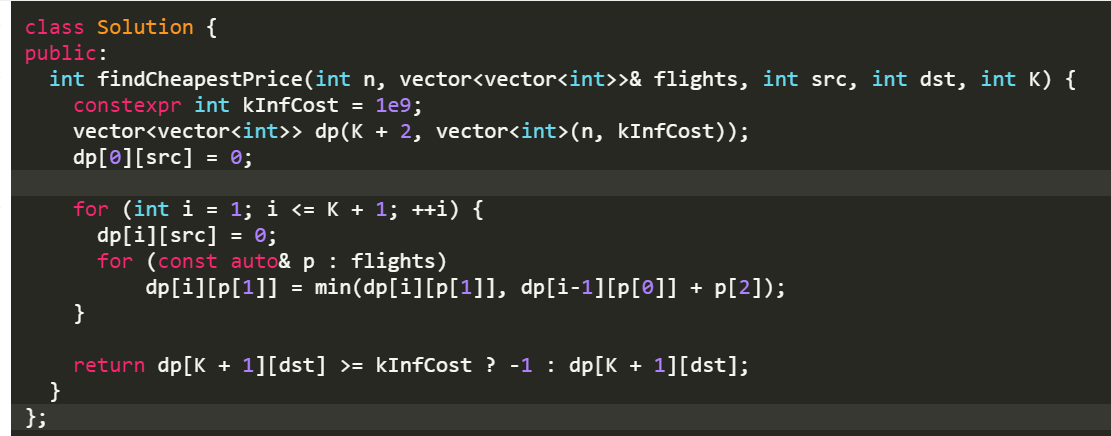
Leetcode 787 Cheapest Flights Within K stops

Bellman-Ford Algorithm

 vector<int,vector<int>> BFA(K+2, vector<int> (n, cost_max);
  k = at most k intermedia points between source 
and destination

Leetcode 198 213 House Robber

DP[i] 表示在1,…,i站下的最大值

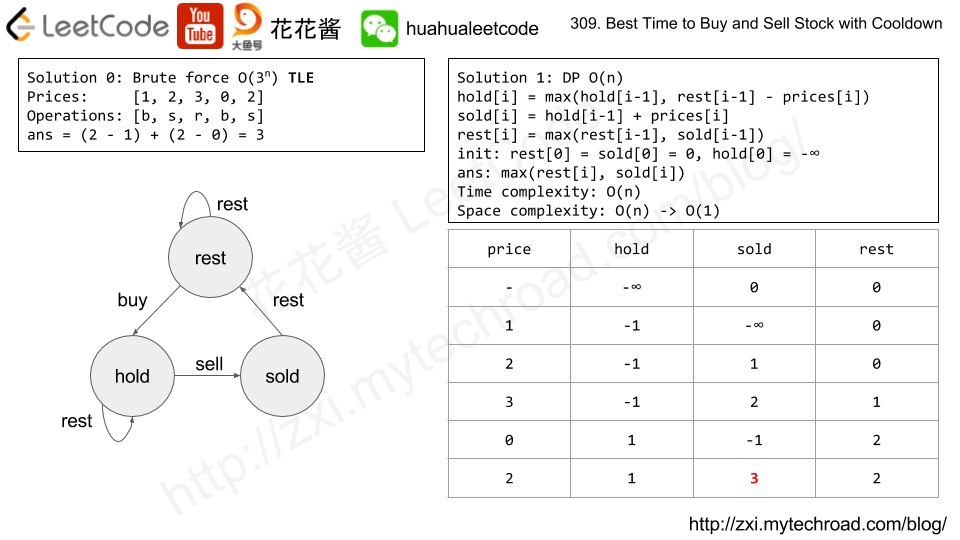
Leetcode 309 Best Time to But and Sell Stock with cool down

DP 用不同的数组表示当前不同的状态 比如买股票，买进，休息，卖出 选公司，选A，选B，这样一直在这些数组间更新对大值

Leetcode 740 delete and earn

想办法转换成其他经典DP问题 比如 Leetcode 740 delete and earn 可以转化成 house robber, 相邻的不能选

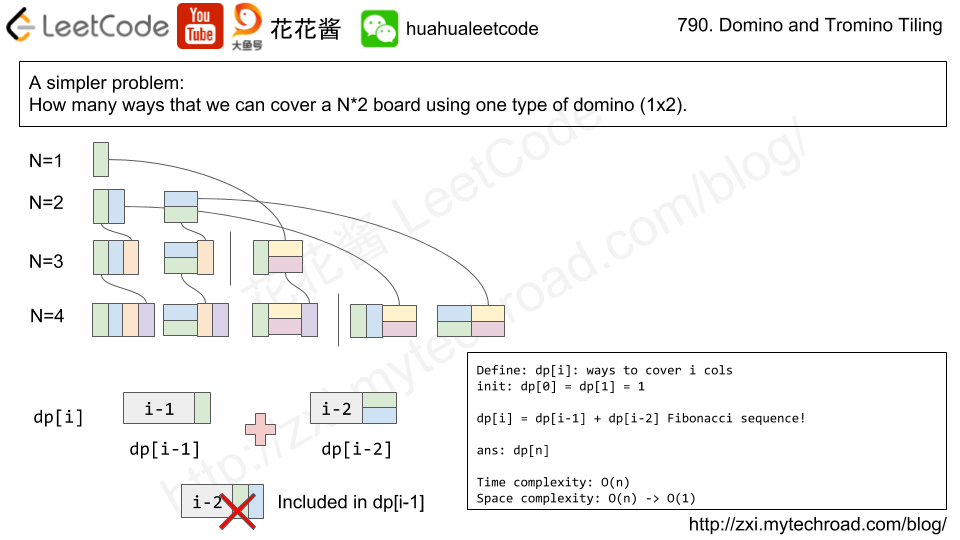
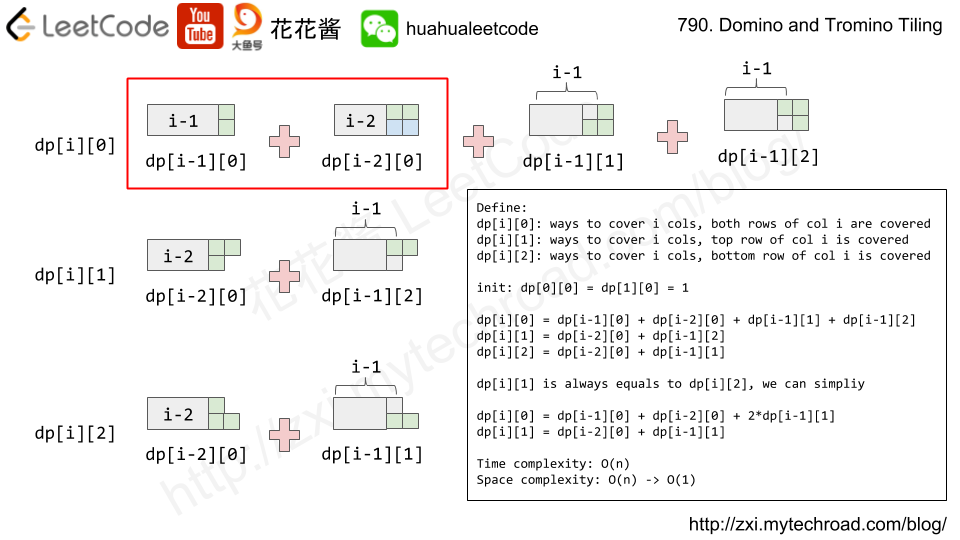
Leetcode 790 Domino and Tromino Tiling

类似题目 模板 跟上面类似，用不同状态 表示DP,看不同状态之间怎么转

堆砌模板 类似于fibinacci

dp[0][0] = dp[1][0] = 1;
dp[0][1] = dp[1][1] = 0;

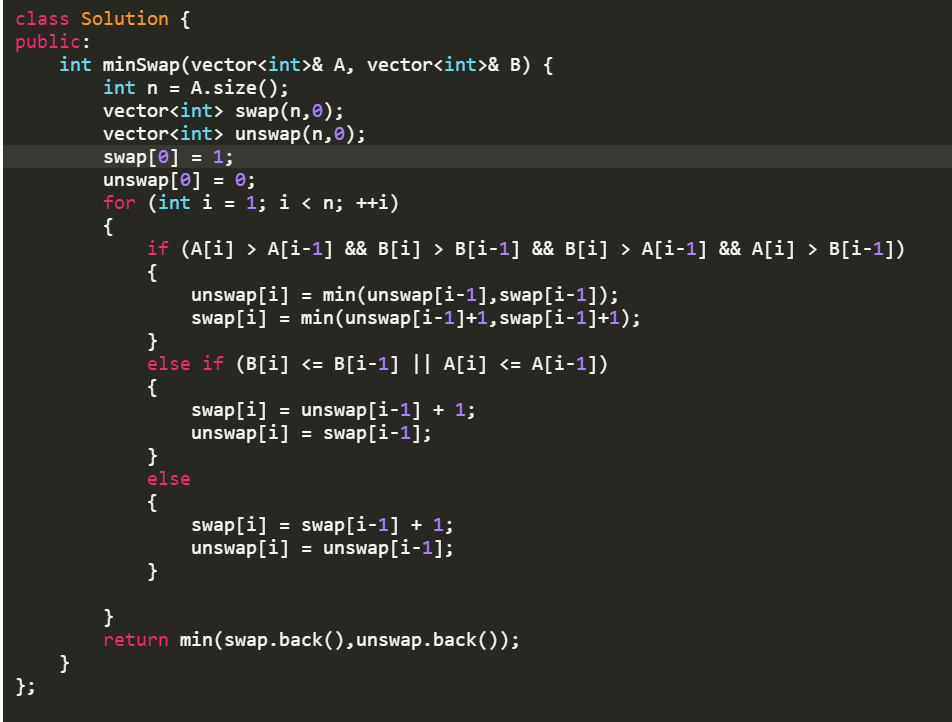
Leetcode 801 swap or not swap

两种状态，两个DP list

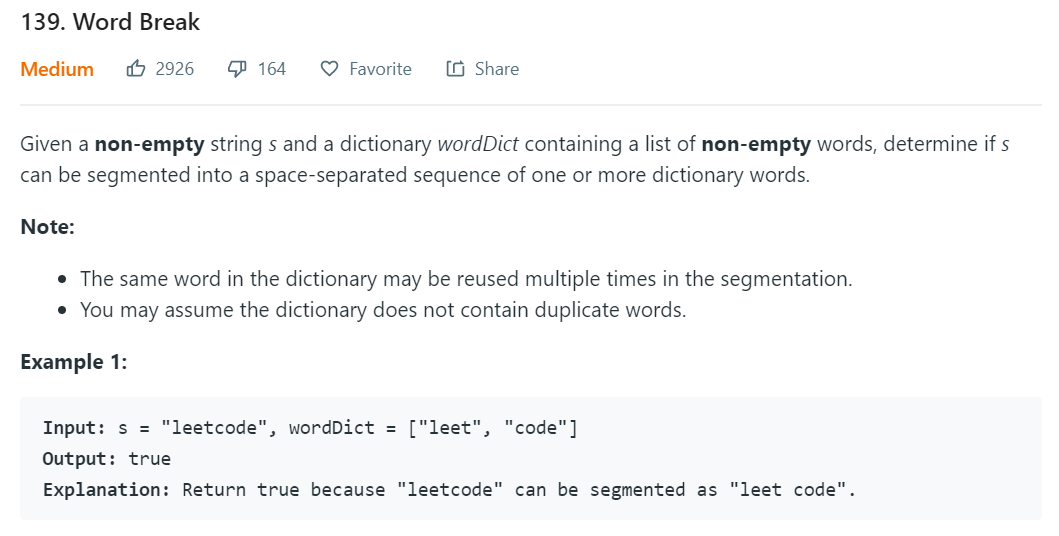
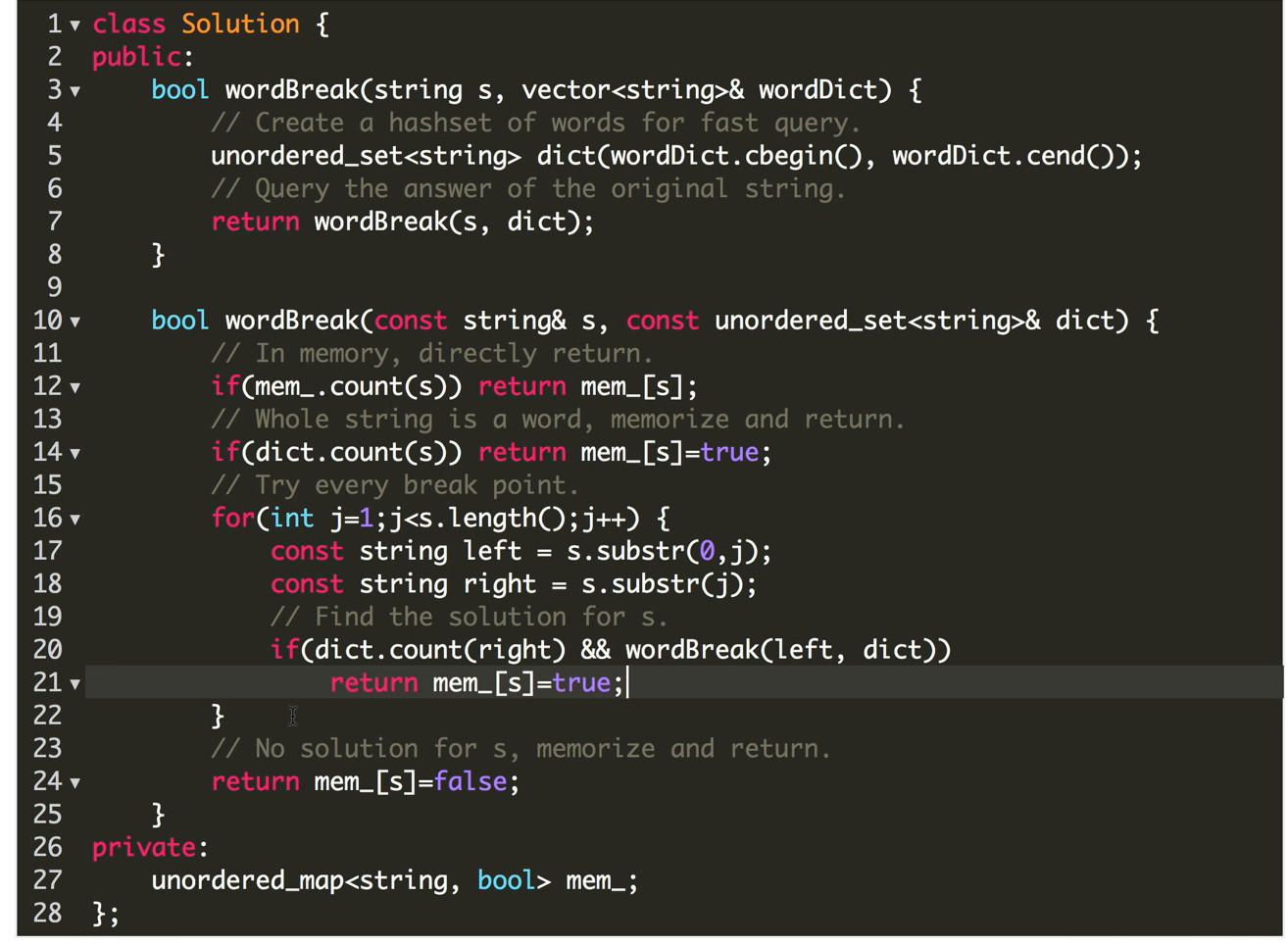
Leetcode 139 Word Break

隔板问题，也可以根据之前的结果进行分析；在这里隔板&&之前是true ；递归也是变相的DP, memorization DP

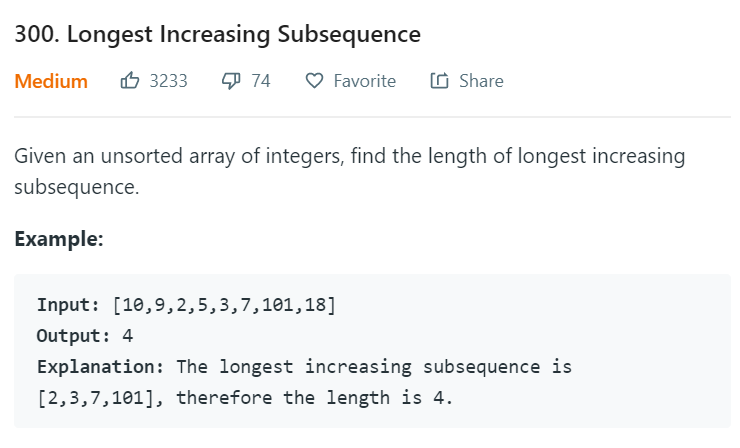
Leetcode 300 Longest Increasing Substring

最长子序列，N*N iteration, DP[i] 以 I 结束的最长子序列 DP[i] iteration 寻找最大值，可以用 max(DP[i], DP[j] + 1); 不断更新自己

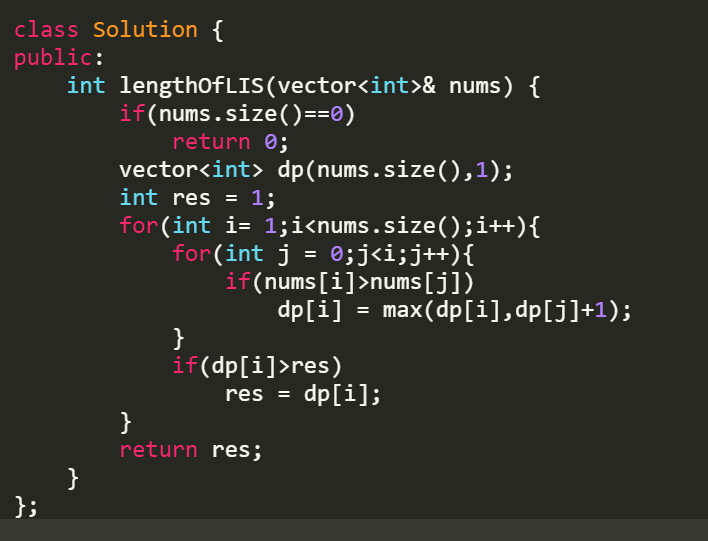
一维数组解决

DP[j] = DP[j](up) + DP[j-1](left);

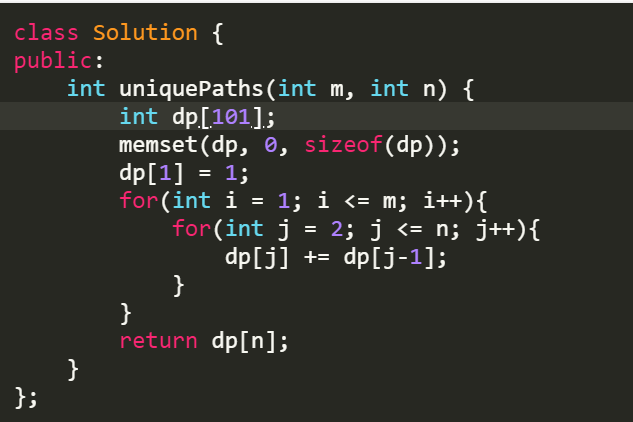
Leetcode 322 coin Change

Classical Coin Change –> First coins and them amount 滚动数组：需要用新的vector保存当前的，然后和之前的交换，滚动进行

• 多少个硬币种类，多少个步骤等等
• 能够用无数个当前的硬币，所以可以用一个dp要不然需要一个tmp，保存之前的dp，这样方便调

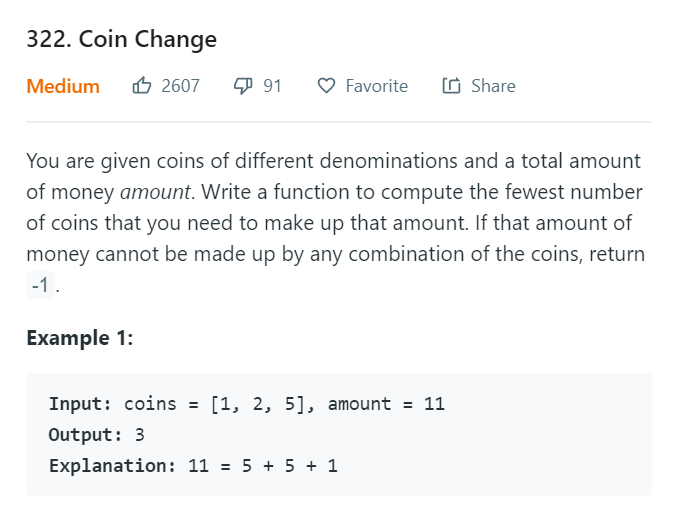
Leetcode 416 Partition Equal Subset Sum

倒过来遍历，这样可以避免重复

for (int i = sum; i >= 0; --i)
{
    if (dp[i]) dp[i+num] = 1;
}

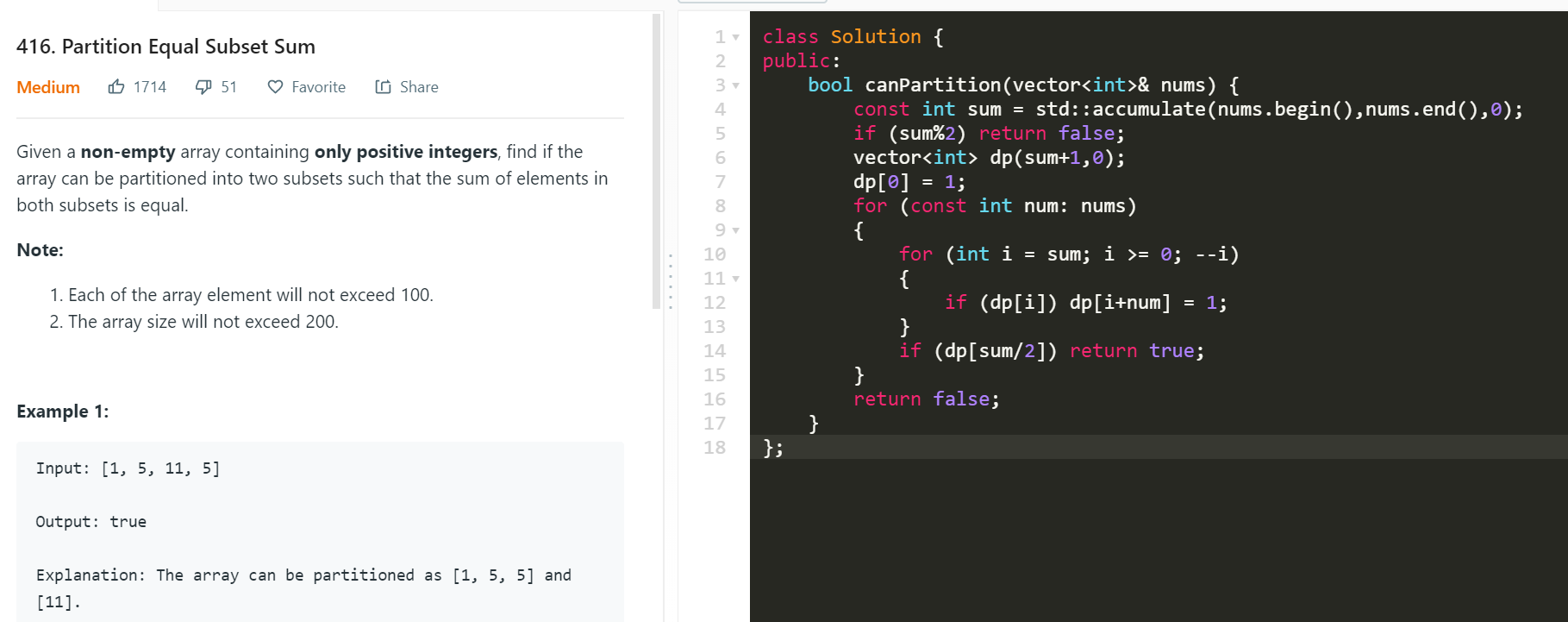
降低空间复杂度

滚动数组降低空间复杂度 用小的值作为外循环 只需要k-1

K  = 1, 2, 3,….
or Coins = 1, 2, 3,…
for (int coin: coins)
{
    // codes
}

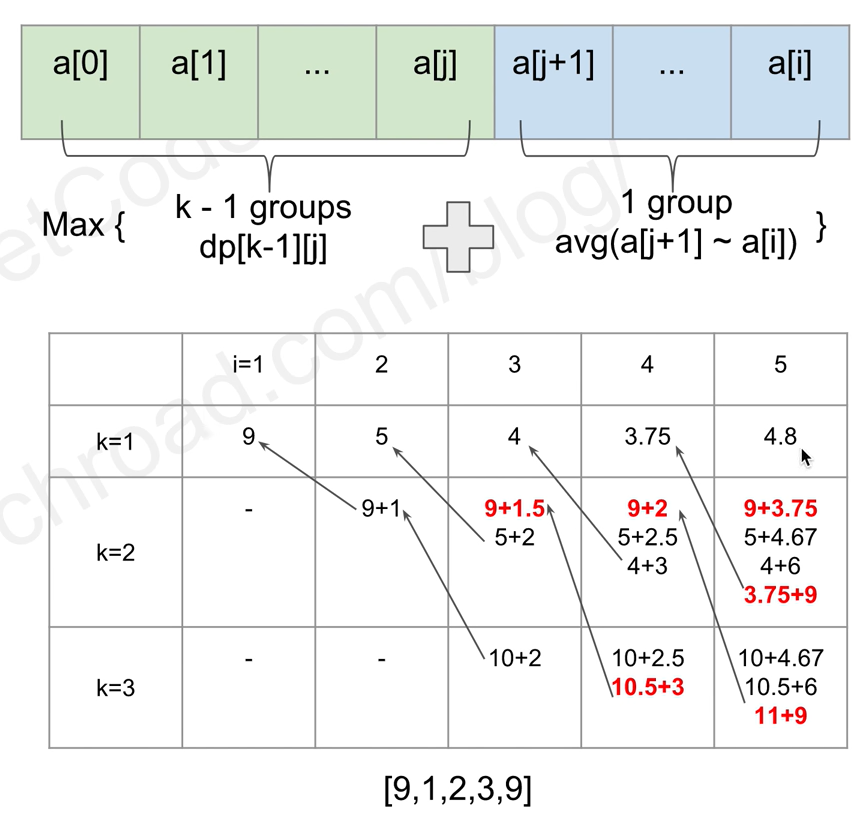
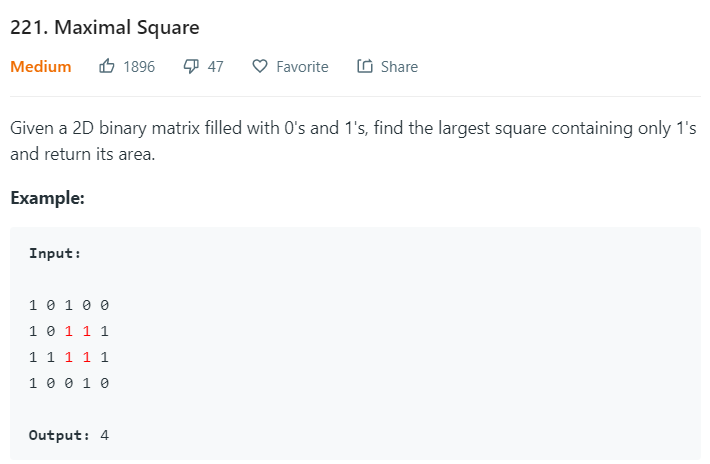
Leetcode 221 Maximal Square

技巧： 从大到小开始计算，希望得到大的值，所以从大的开始 全部看成右下角

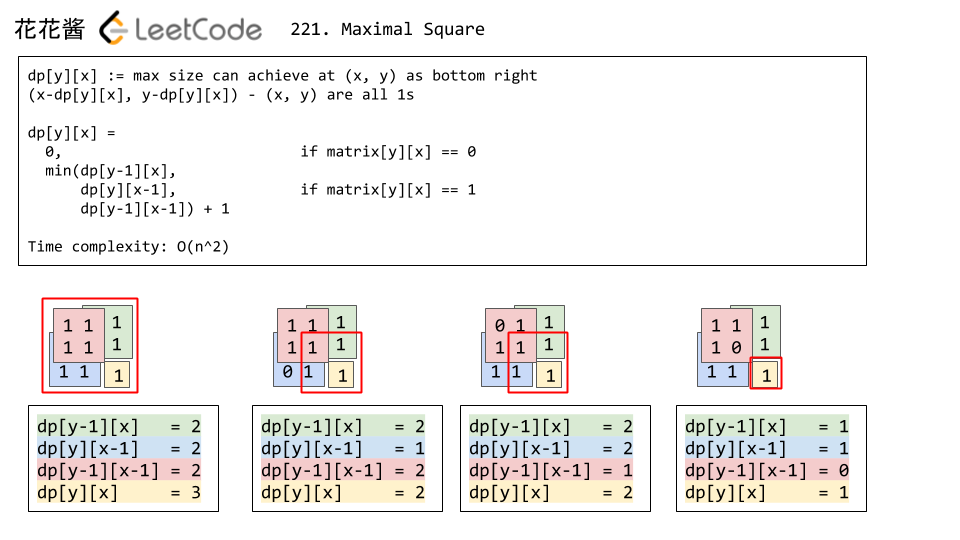
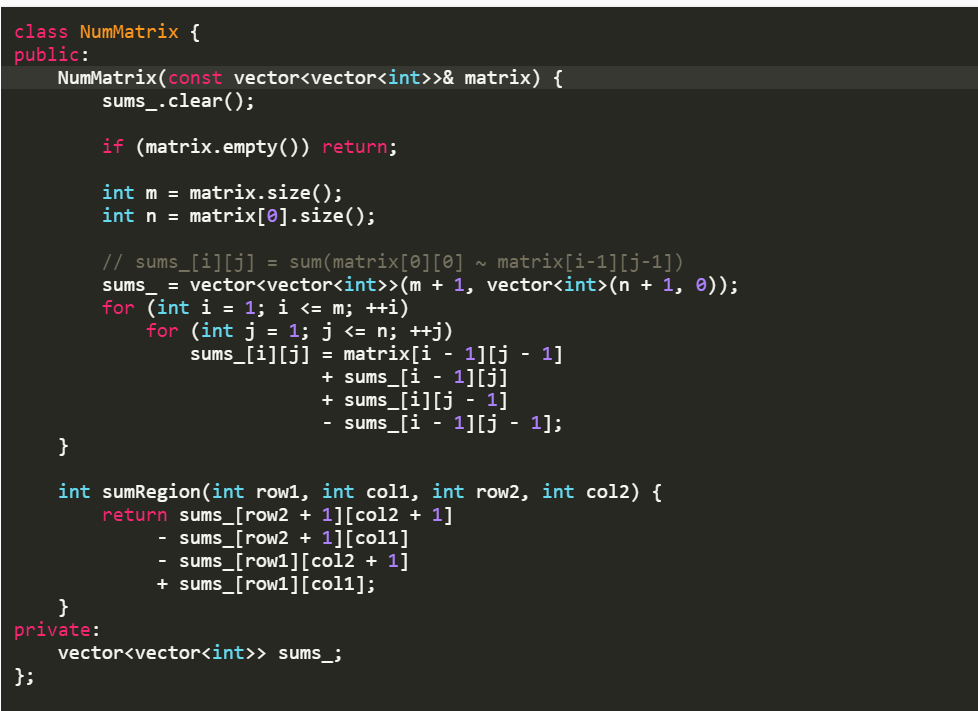
Leetcode 304 Range Sum Query 2D - Immutable

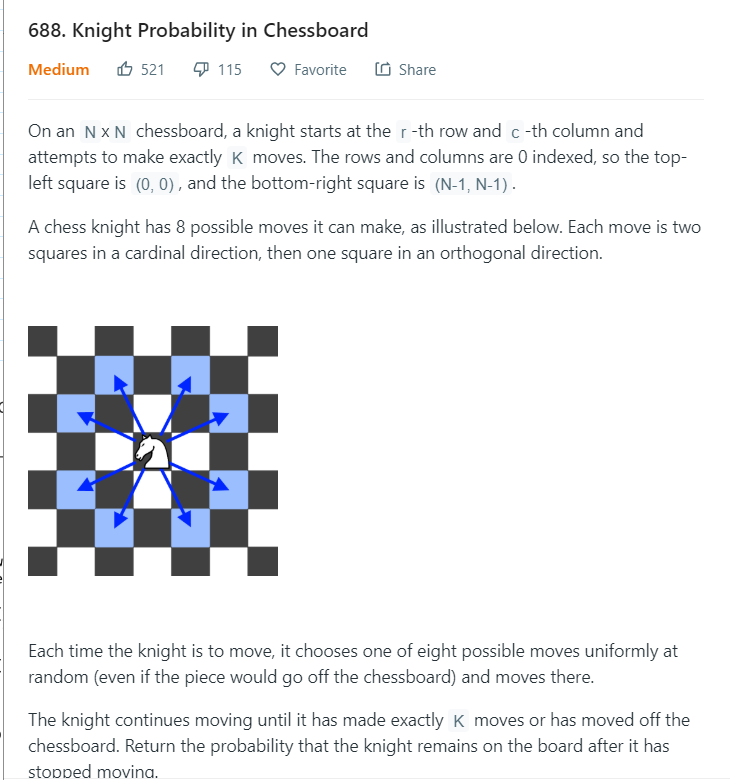
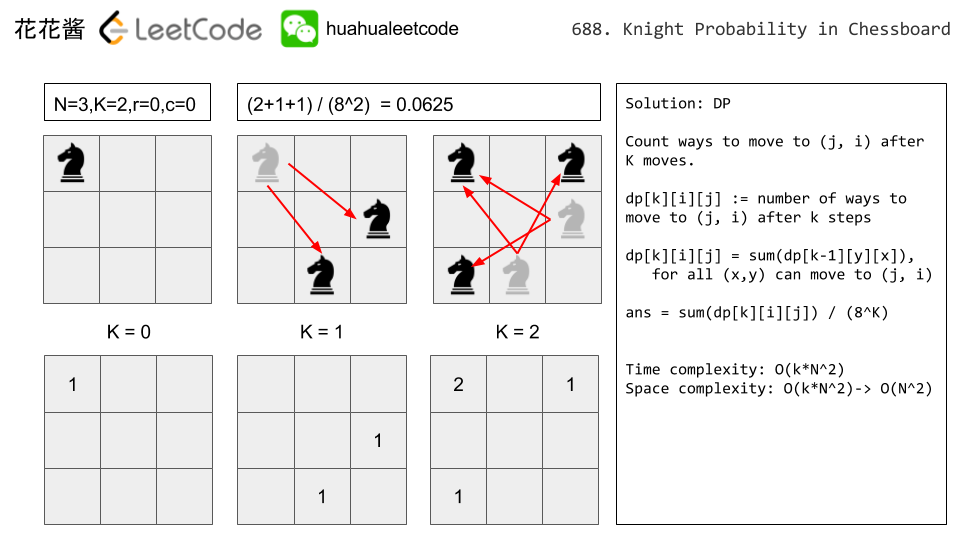
Leetcode 688 Knight Probability in ChessBoard

Leetcode 576 Out of Boundary Paths

Leetcode 120 Triangle

换个方向思考，反着来； 从外面到里面，从上到下，DP

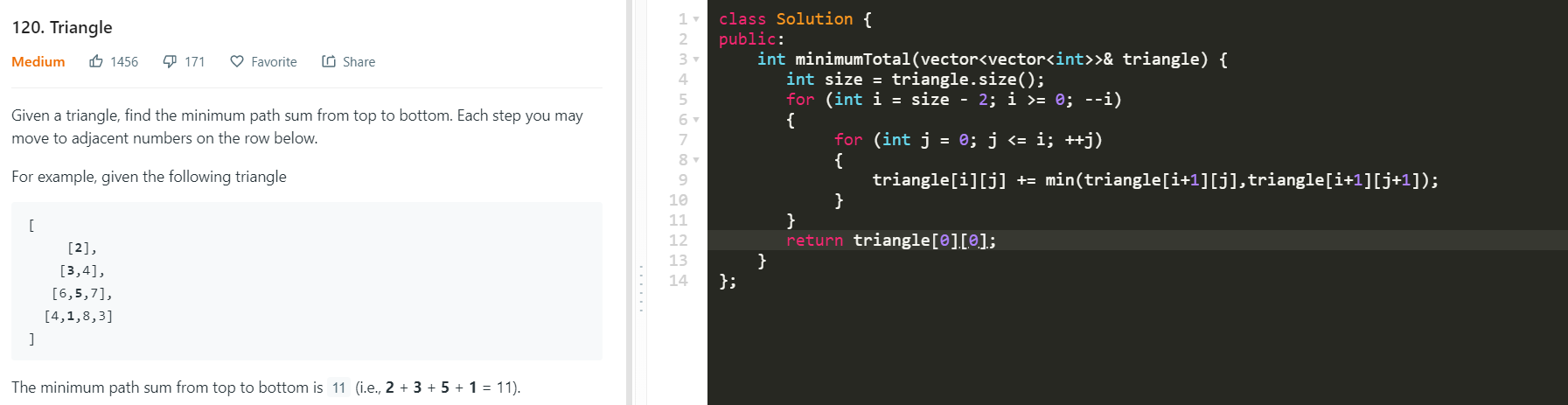
DP Push or Pull

sometimes, Push is faster because of pruning some processes

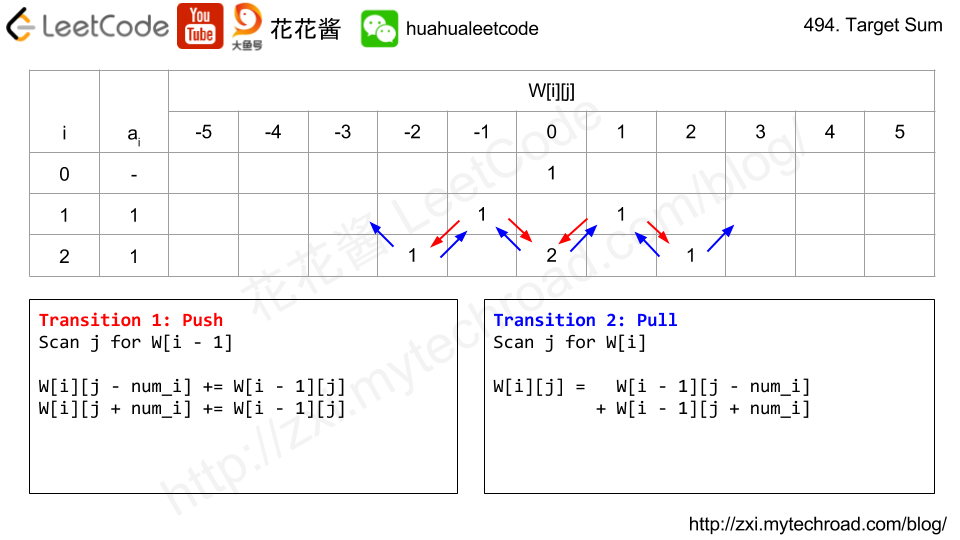
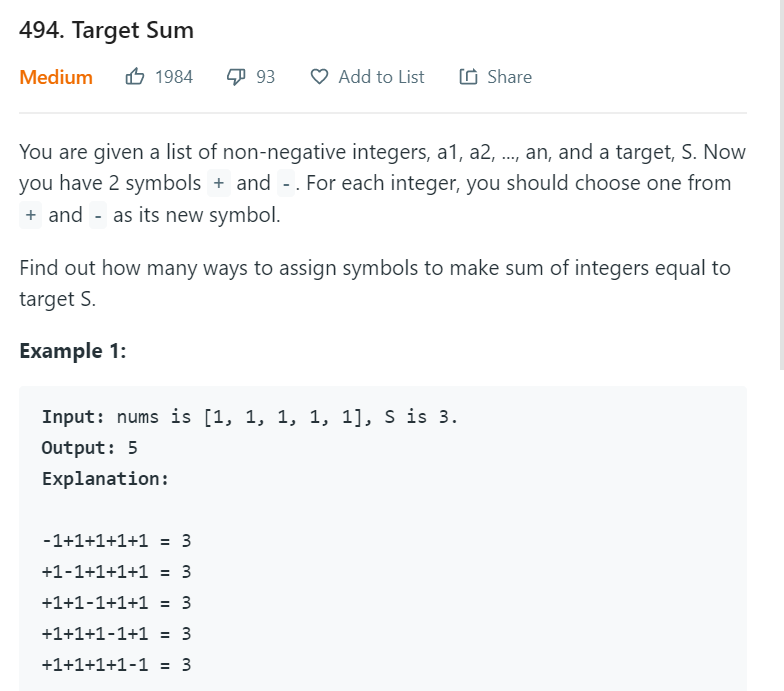
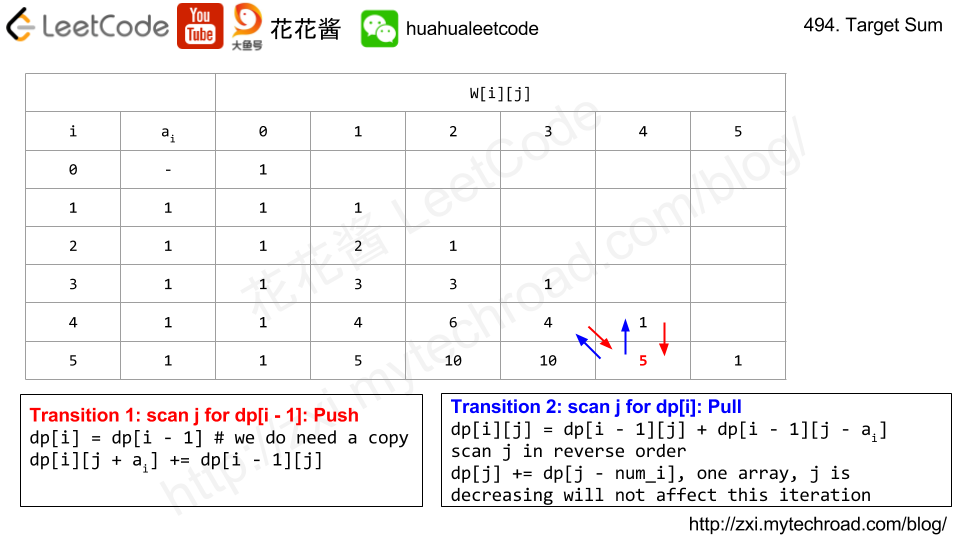
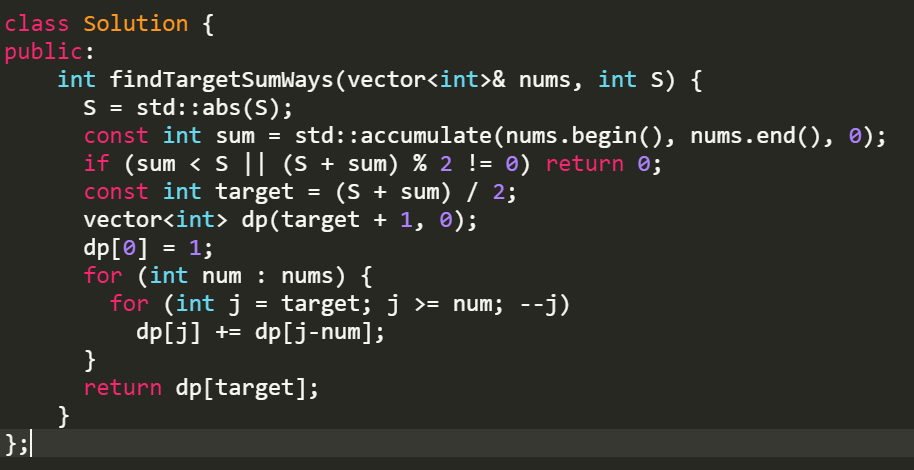
Leetcode 494 Target Sum

DP一维数组！！！0-1 背包问题

只依托比当前index小的数组的话，就可以只用一个数组，或者反向也可以

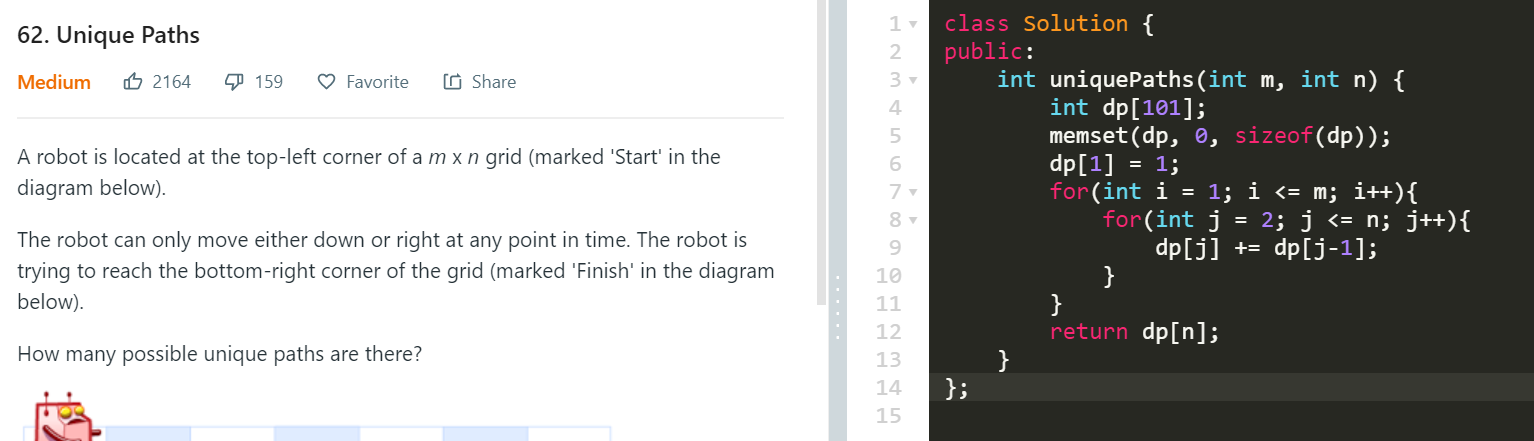
Leetcode 62 Unique Paths

DP一维数组！！！0-1 背包问题

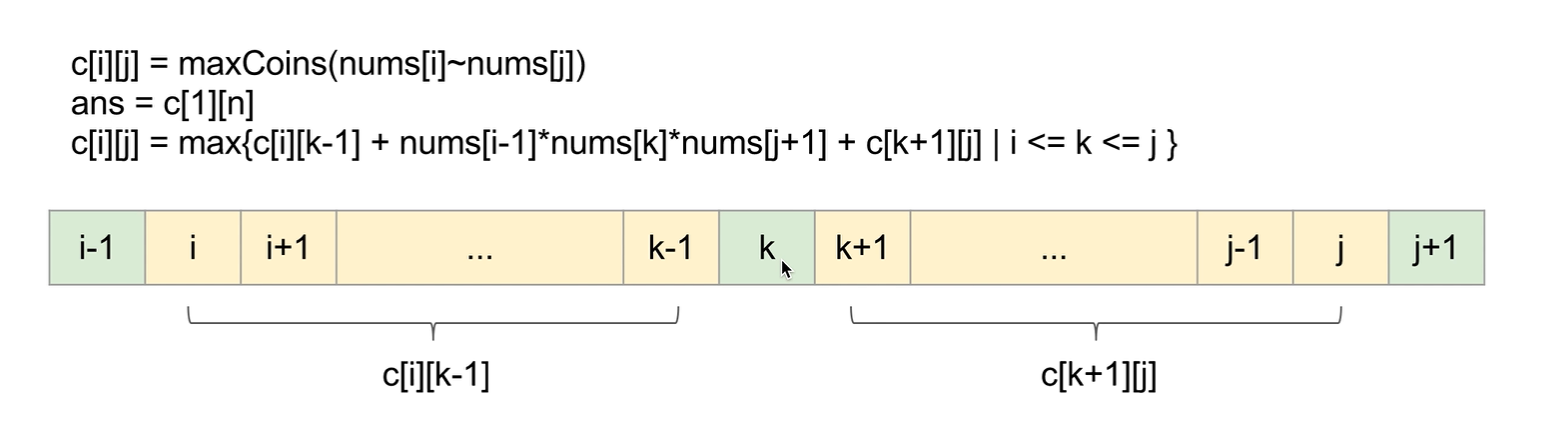
Leetcode 312 Burst Balloons

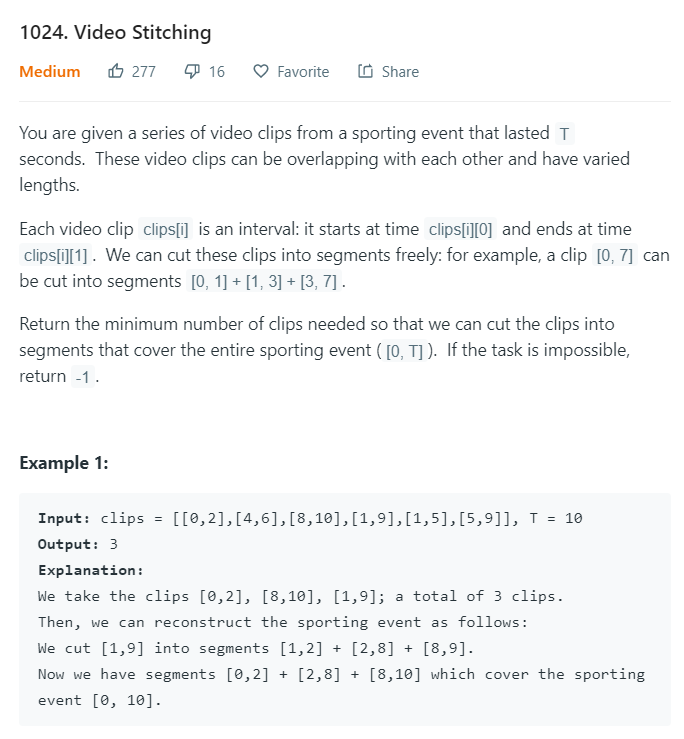
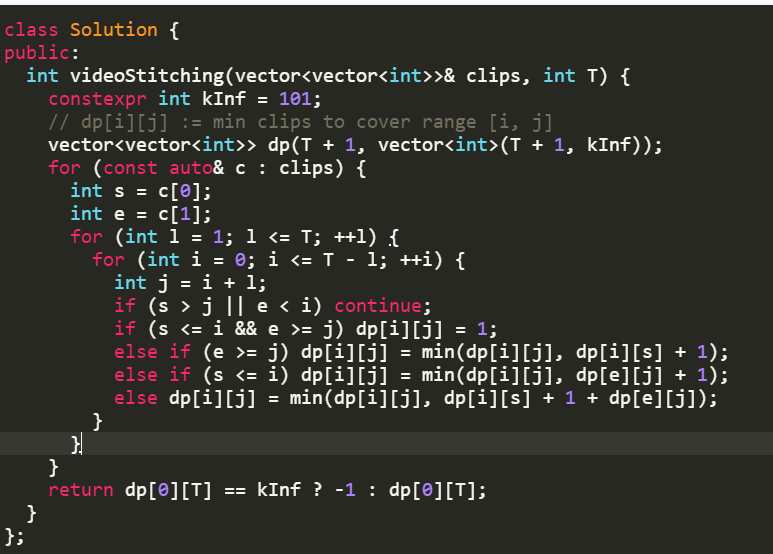
Leetcode 1024 Video Stitching

• Previous
  Leetcode Array
• Next
  Leetcode General