Representation


Keys:
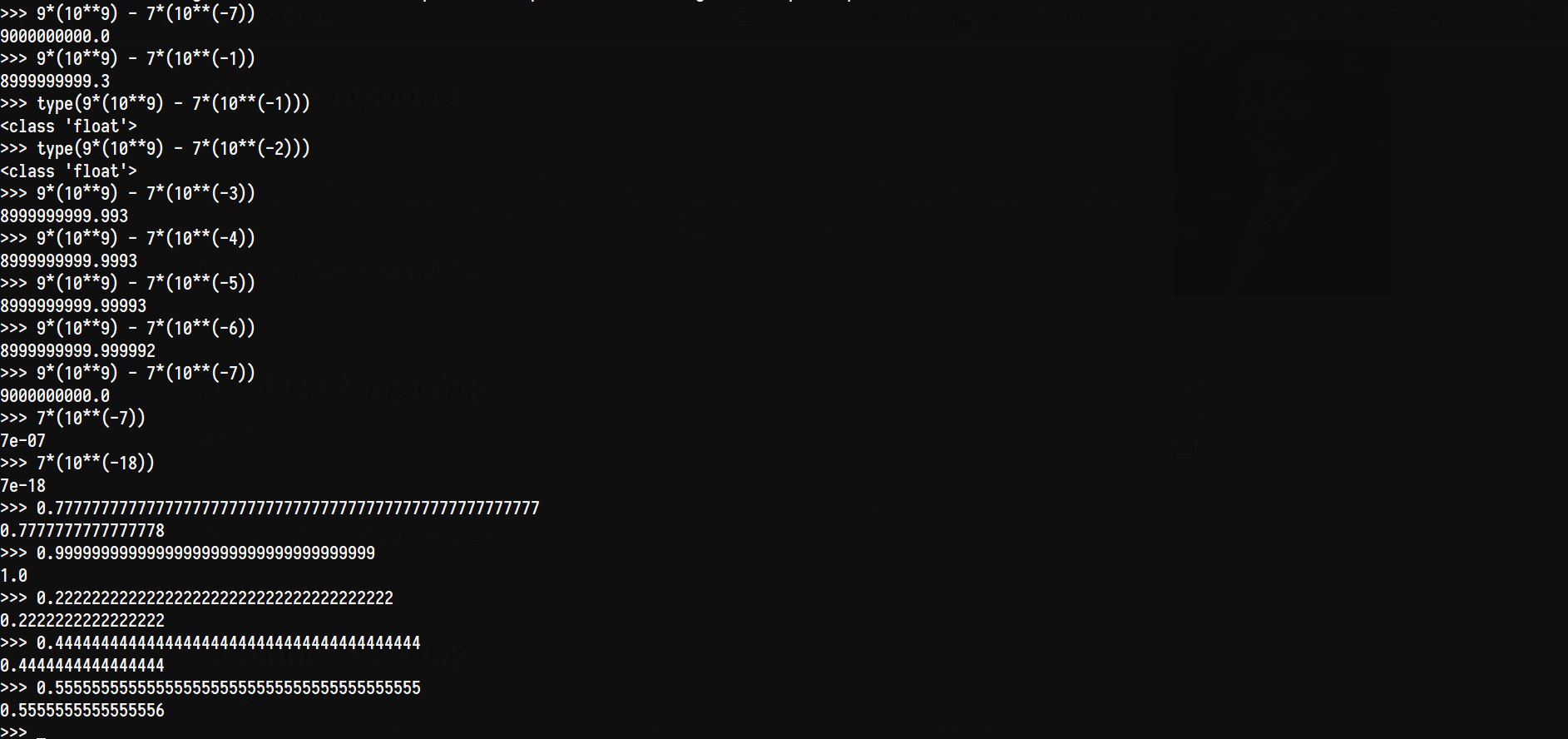
0.1 vs 0.5
0.1 不能被完全表示;因为十进制的0.1换算成二进制是一个无限循环小数 0.5 可以 因为是二进制的小数 2 的 -1 次方
float == float ??
由于浮点数存在运算误差,所以比较两个浮点数是否相等常常会出现错误的结果。正确的比较方法是判断两个浮点数之差的绝对值是否小于一个很小的数
如果参与运算的两个数其中一个是整型,那么整型可以自动提升到浮点型号.
浮点数常常无法精确表示,并且浮点数的运算结果可能有误差;
比较两个浮点数通常比较它们的绝对值之差是否小于一个特定值;
整型和浮点型运算时,整型会自动提升为浮点型;
可以将浮点型强制转为整型,但超出范围后将始终返回整型的最大值。
溢出
浮点数有上溢区和下溢区之分,当浮点数的阶码大于最大阶码时,称为上溢,此时机器停止运算,进行溢出中断处理;如果阶码小于最小的阶码时,称为下溢, 此时溢出的数值非常小,直接强制将浮点数的尾数置为0,可以继续执行运算。
规格化
浮点数的规格化
基数为2时,尾数最高为1的数规格化数。规格化时,尾数左移一位,阶码减1;尾数右移一位,阶码加1。当尾数小于等于1的时候,规格化就完成了。
我们来看看如何将一个数规格化成浮点数(包括其原码、反码、补码):
例子:设浮点数字长为16位,其中阶码5位,尾数11位,令x=-54,请将其规格化为基数为2的浮点数 1)先将-54转换为二进制形式:-110110 2)规格化得到-(0.1101100000)* 2^110^ 3)得到在浮点机中的结果:[x]~原~ = 0.0110;1.1101100000,[x]~补~=0.0110;1.0010100000,[x]~反~=0.0110;1.0010011111.
原码就是:one’s complement 我们希望 (+1)和(-1)相加是0,但计算机只能算出0001+1001=1010 (-2)
反码:为了解决“正负相加等于0”的问题,在“原码”的基础上,人们发明了“反码”。“反码”表示方式是用来处理负数的,符号位置不变,其余位置相反。有两个零存在,+0 和 -0
补码:two’s complement “补码”的意思是,从原来”反码”的基础上,补充一个新的代码,(+1)
浮点数加减运算
•“对阶”操作:目的是使两数阶码相等
–小阶向大阶看齐,阶小的那个数的尾数右移,右移位数等于两个阶码差的绝对值
–IEEE 754尾数右移时,要将隐含的“1”移到小数部分,高位补0,移出的低位保留到特定的“附加位”上
1)对阶,使得两数的小数点位置对齐。低阶向高阶看齐。 2)尾数求和,将对阶后的两个尾数按照定点的加减法运算规则计算。 3)规格化,为增加有效数字的位数,提高运算精度,必须将求和(差)后的尾数规格化 4)舍入,为提高精度,要考虑尾数右移时候丢失的数值位 5)溢出判断,判断计算结果是否存在溢出
浮点数的乘数法运算
1)阶码相加减:按照定点整数的加减法运算方法对两个浮点数的阶码进行加减运算。
2)尾数相乘或相除:按照定点小数的阵列乘除法运算方法对两个浮点数的尾数进行乘除运算。为了保证尾数相除时商的正确性,必须保证被除数尾数的绝对值一定小于除数尾数的绝对值。若被除数尾数的绝对值大于除数尾数的绝对值,需对被除数进行调整,即被除数的尾数每右移1位,阶码加1,直到被除数尾数的绝对值小于除数尾数的绝对值。
3)结果规格化并进行舍入处理:浮点数乘除运算结果的规格化和舍入处理与浮点数加减运算结果的规格化和舍入处理方法相同。并且在浮点数乘除运算的结果中,由于乘积和商的绝对值一定小于1,因此在浮点乘除运算结果进行规格化处理时只存在向左规格化,不可能出现向右规格化。
4)判断溢出:浮点数乘除运算结果的尾数不可能发生溢出,而浮点数运算结果的溢出则根据运算结果中浮点数的阶码来确定,溢出的判定和处理方法与浮点加减运算完全相同。
例子:设两浮点数x=2-001×(-0.100010),y=2-100×(0.010110),求x*y [x]~浮~=11111,1.011110 [y]~浮~=11100,0.010110
float double
范围
float和double的范围是由指数的位数来决定的。 float的指数位有8位,而double的指数位有11位,分布如下: float: 1bit(符号位) 8bits(指数位) 23bits(尾数位) double: 1bit(符号位) 11bits(指数位) 52bits(尾数位) 于是,float的指数范围为-127~+128,而double的指数范围为-1023~+1024,并且指数位是按补码的形式来划分的。 其中负指数决定了浮点数所能表达的绝对值最小的非零数;而正指数决定了浮点数所能表达的绝对值最大的数,也即决定了浮点数的取值范围。 float的范围为-2^128 ~ +2^128,也即-3.40E+38 ~ +3.40E+38;double的范围为-2^1024 ~ +2^1024,也即-1.79E+308 ~ +1.79E+308。
精度
float和double的精度是由尾数的位数来决定的。浮点数在内存中是按科学计数法来存储的,其整数部分始终是一个隐含着的“1”,由于它是不变的,故不能对精度造成影响。 float:2^23 = 8388608,一共七位,这意味着最多能有7位有效数字,但绝对能保证的为6位,也即float的精度为6~7位有效数字; double:2^52 = 4503599627370496,一共16位,同理,double的精度为15~16位。